Associative and Commutative property of Addition in Coq

In this blog post, I’ll be going over associative and commutative property of addition. Also, I’ll be going over how to prove that using Coq. But first of all, what is addition?

Addition

We all know what addition is but I’ll still explain it in brief. In mathematics, addition is the process of adding two or more numbers together to find the final result. Addition is represented by the + symbol. For example: 1 + 1 equals 2, 10 + 10 equals 20 so on.

In programming perspective, think of + as a function that takes in two arguments of type number(Integer) and adds them together and returns the result. Now we know what addition is let’s take a look at some properties of addition.

Induction

Before looking into the properties of addition, let’s first take a look at what induction is. Because we are going to use proof by induction method to solve the theorems/proofs.

What is Proof by Induction?

“Mathematical Induction is a method for proving that a statement P(n) is true for every natural number n, that is, infinitely many cases P(0), P(1), P(2), P(3)…..P(n) all hold. This is done by first proving a simple case, then also showing that if we assume the claim is true for a given case, then the next case is also true.” — From Wikipedia.

If we break this down step by step, Mathematical induction contains two steps.

1. Show it is true for the first one.
2. Show that if any one is true then the next one is true.

Then all are true.

Induction step 1

We have to prove the base case, ie., n = 0 or n = 1.

Induction step 2

• Assume it is true for n = k, where k is an arbitrary number.
• Prove it is true for n = k + 1 (we can use the n = k as a fact).

We’ll see how this(induction) works out when proving the associative and commutative property of addition

Associative property

Associative property of addition states that, no matter how a set of three or more numbers are grouped together, the sum remains the same.

For example, if a, b and c are natural numbers then a + (b + c) = (a + b) + c. Let’s apply some natural numbers to a, b and c.

Let a = 10, b = 20 and c = 30, therefore:

10 + (20 + 30) = (10 + 20) + 30
10 + 50 = 30 + 30
60 = 60

This is associative property in a nutshell. In the above example, we’ve only taken three numbers a, b and c but it can be more as well.

Okay, now that we know the associative property of addition, let’s prove that using Coq.

(* Prove associative proerty of addition *)
Theorem proving_add_associative: forall a b c: nat, a + (b + c) = (a + b) + c.
    Proof.
    intros a b c.
    induction a as [| a' IHa'].
    - simpl. reflexivity.
    - simpl. rewrite IHa'. reflexivity.
    Qed.

The above theorem states that, for all natural numbers a, b and c, a + (b + c) is equal to (a + b) + c.

Between the Proof and Qed tactic is where we write our proof. Since we have three variables a, b and c, we have to bring them into our proof. To do that, we can use the intros tactic which is short for introduction or introduce.

induction

The line induction a as [| a' IHa']. does induction on variable a. When induction is applied on a, we have two cases to prove.

1. When a = 0
2. When a = k, where k is an arbitrary number.

In the above command, we have two things mentioned inside the square brackets( [] ). These are the names of the variables we assigned as part of induction. Our base case is a = 0, so we don’t have to assign/create any variable for that. For our second case, a = k we have to create a variable to hold the arbitrary number, for that we have created a variable named a’.

What is IHa’?

IH is short for Induction Hypothesis. And IHa’, a’ is added in the name because this hypothesis is for a’. So for readability we have named it as IHa’. You can name the variables whatever you want. I could’ve done like this as well [| k' IHk'].

Going further

Now, let’s see what is the state of our theorem when we execute the intros. tactic and induction tactic.

As you can see, after applying proof by induction we have two goals.

1. When a = 0
2. When a = S a’, where S a’ is an arbitrary number.

Now, lets solve the first goal. We can focus on the goal using - sign.

We know that 0 plus anything equals anything. In this case, on the left hand side we have 0 + (b + c) and on the right hand side we have 0 + b + c. So, we can simplify the LHS and RHS like b + c = b + c using the simpl. tactic, which gives us

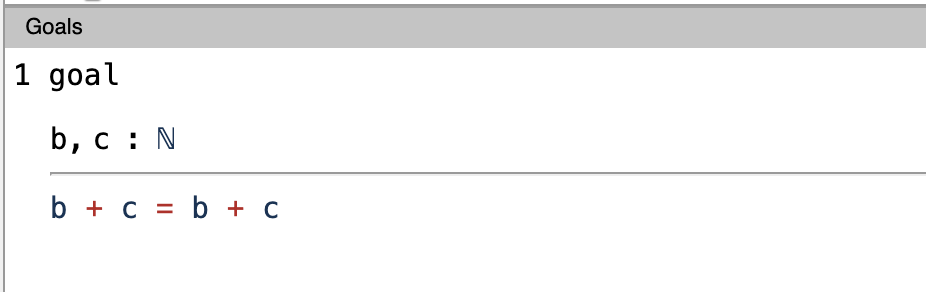
Now we can use reflexivity. tactic to prove the equality. Since both LHS and RHS are equal, executing the reflexivity tactic would solve our first goal.

Let’s focus on our second goal using the - .

In our second goal, we have to prove S a' + (b + c) = S a' + b + c. We also got an induction hypothesis(IHa'), which states that a' + (b + c) = a' + b + c. Here, we’ve assumed that this hypothesis is true, so that we can use this hypothesis to prove our goal.

Let’s use the simpl. tactic to simplify both LHS and RHS.

Executing the simpl. tactic grouped our variables. If you look at LHS, we have a' + (b + c). In our induction hypothesis we have assumed that a' + (b + c) = a' + b + c is true. Therefore, we can use this hypothesis to prove our goal.

Let’s rewrite our statement using the induction hypothesis. We can use the rewrite. tactic to do this. Executing rewrite IHa' results in

As you can see, we’ve replaced(rewrote) a' + (b + c) with a' + b + c, because we have assumed a' + (b + c) = a' + b + c to be true. Now if you look at both LHS and RHS, its equal. We can check the equality property using the reflexivity. command.

Boom! we’ve proved the associative property of addition.

Commutative property

I’m too lazy to add the images to explain each and every step, so I'm planning to make a video explaining things. Will be uploading soon once the blog goes live!

References

• Induction: https://en.wikipedia.org/wiki/Mathematical_induction
• Associative property: https://en.wikipedia.org/wiki/Associative_property
• Commutative property: https://en.wikipedia.org/wiki/Commutative_property