Modelling and Proving logic gates in Coq

In this post, we’ll explore how to model primitive logic gates such as AND, OR and NOT in Coq. Furthermore, we’ll take an additional step by proving their properties. First of all what is Coq?

DISCLAIMER: I’m not an expect in Coq. I’m learning it out of curiosity. So whatever I’m saying in this post, take it with a grain of salt.

Coq

Coq is a functional programming language which is also a proof assistant used for formal verification and theorem proving. It provides a formal language for expressing mathematical statements and proofs.

I’m not gonna go into Coq as there are many resources available online if you want to learn. I’m gonna only focus on modelling the logic gates and proving their properties. I highly recommend you to follow along by writing code. Use the Coq online interpreter to write code. We’ll be doing two things.

1. Model all the three primitive logic gates(AND, OR and NOT)
2. Prove the properties of the primitive gates we modelled.

First, let’s focus on modelling them.

And gate

Let’s first look at the truth table of AND gate.

| A | B | OUT |
|---|---|-----|
| 0 | 0 | 0   |
| 0 | 1 | 0   |
| 1 | 0 | 0   |
| 1 | 1 | 1   |

By looking at the above truth table, we can tell that:

1. If both the inputs are true, then the output is true.
2. If any one of the input is false then the output is false.

Now, let’s model it in Coq.

Definition AND (a: bool) (b: bool): bool := 
    match a with
    | true => b
    | false => false
    end.

In the above code, we created a Definition, which in imperative programming languages we call it functions. The name of the definition is AND, which takes two arguments of type boolean. We are doing pattern matching expression in the body of the definition.

1. a is the term being matched.
2. true and false are the patterns being matched against a
3. b is the expression to be evaluated if a matches true
4. false is the expression to be evaluated if a matches false

By using the match construct, we we’re able to pattern match the expression and model the AND gate.

OR gate

Let’s first look at the truth table of OR gate.

| A | B | OUT |
|---|---|-----|
| 0 | 0 | 0   |
| 0 | 1 | 1   |
| 1 | 0 | 1   |
| 1 | 1 | 1   |

By looking at the above truth table, we can tell that

1. If both the inputs are false, then the output is false
2. If any one of the input is true, then the output is true.

Now, let’s model it in Coq.

Definition OR (a: bool) (b: bool): bool :=
    match a with
    | true => true
    | false => b
    end.

The name of the definition is OR, which takes two arguments of type boolean.

1. a is the term being matched.
2. true and false are the pattern being matched against.
3. b is the expression to be evaluated if a matches false
4. true is the expression to be evaluated if a matches true

NOT gate

Let’s first look at the truth table of NOT gate

| A | OUT |
|---|-----|
| 0 | 1   |
| 1 | 0   |

By looking at the above truth table, we can tell that

1. If the input is 0(false), then the output is 1(true)
2. If the input is 1(true), then the output is 0(false)

Now, let’s model it in Coq.

Definition NOT (a: bool): bool :=
    match a with
    | true => false
    | false => true
    end.

The name of the definition is NOT, which takes in one argument of type boolean.

1. a is the term being matched.
2. true and false are the pattern being matched against
3. false is the expression to be evaluated if a matched true
4. true is the expression to be evaluated if a matched false

Now that we’ve modelled the primitive gates, let’s prove their properties. In simple terms, think of it like a test case that we would write to test some functionality. In this case, we’ve modelled primitive gates like a function that would return something based on the input. So, we would be proving if the function we’ve created works as expected or not.

Proving NOT gate property

Let’s first prove NOT gate, because we only have to prove couple of cases. In Coq, we’ll use the Theorem command to prove mathematical theorem or properties. Theorem is used to declare propositions that we want to prove formally. The thing that we want to prove here is that the property of the NOT definition.

There are two cases we must prove:

1. true = false
2. false = true

Let’s just look at the theorem.

Theorem proving_not: forall (a: bool), NOT (NOT a) = a.
    intros.
    destruct a.
    simpl; reflexivity.
    simpl; reflexivity.
Qed.

There are a lot of thing to breakdown in the above code. Let’s do it one by one.

Theorem

Theorem’s start with the Theorem keyword, followed by the name of the theorem. In this case, the name of our theorem is proving_not. So the syntax would be,

Theorem <name_of_the_theorem>: , followed by what we are trying to prove. In this case, we are trying to prove for all “a”(which is a boolean type), NOT (NOT a) = a, which means, if we expand the NOT (NOT a) definition by replacing a with true or false, the result should be equal to a. For example,

a = true, so
NOT (NOT a) = a => NOT (NOT true)
                => NOT false
                => true

a = false, so
NOT (NOT a) = a => NOT (NOT false)
                => NOT true
                => false                    

When we execute Theorem proving_not: forall (a: bool), NOT (NOT a) = a. , this is what Coq creates for us to prove. It creates a goal, which we should prove. The goal is nothing but, what we stated in our Theorem

intros

intros is a keyword that is part of tactics. What are tactics? Tactics are commands or procedures used to manipulate and reason about proofs within the proof environment.

intros is part of the Introduction tactics. It is used to introduce variables into the proof context. In our case, we have only one variable which is a. So it brings a into the proof context so that we can manipulate it and prove our theorem.

When intros. gets executed, it brings a into the context. This is what happens when it gets executed.

You can see a horizontal line, the things above the line contains variables, hypothesis, etc in the context that we use to manipulate to solve the proof. As you can see here, we have a: bool which is the only variable that belongs in our Theorem. The things below the horizontal line is when we need to prove to achieve our goal.

destruct

destruct keyword is used to perform case analysis on an inductive type, breaking down the proofs into separate cases based on the possible constructors of the type. It is commonly used to reason about values of an inductive type by considering all possible cases individually.

When we execute destruct a. , it creates two subgoals for us to prove.

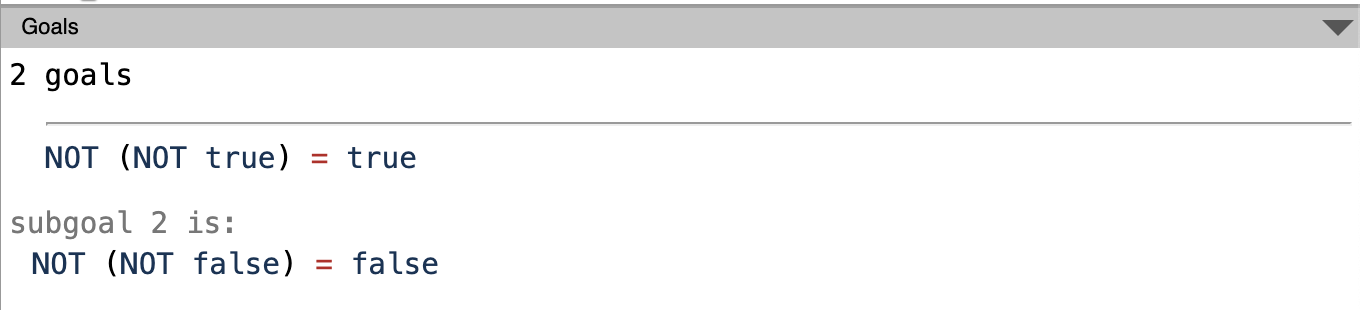
As you can see from the above picture, the destruct tactic breaks down our initial goal into two subgoals because we have to solve for two different cases which is true and false. Now we have to solve these two goals. First we’ll solve NOT (NOT true) = true because that is what is currently in the context.

simpl

simpl keyword is short for simplify. We use this tactic to simplify the expression in the proof context by performing computation and reduction according to the definitions of the involved terms. For example, In our case we have an expression NOT (NOT true) . What simpl does is reduce the expression recursively until it cannot be reduced further. If we reduce this expression:

NOT (NOT true) => NOT (false) => true

If we run the simpl. command this is what we get:

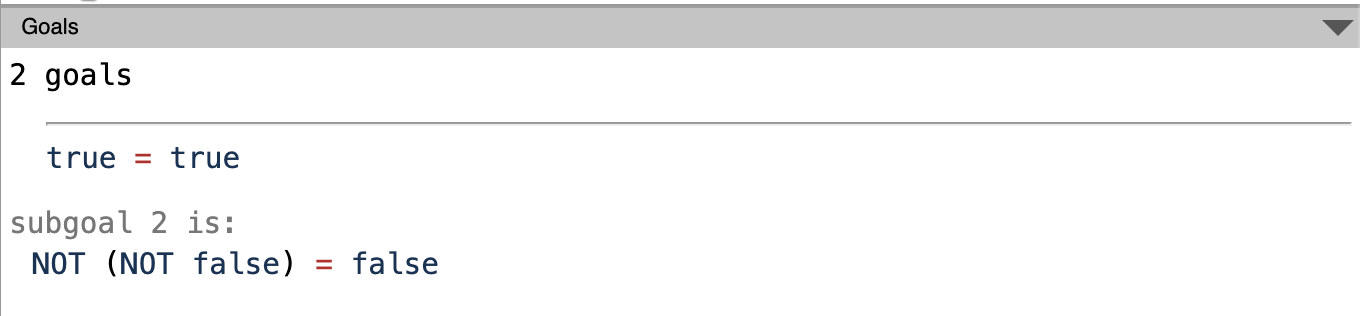
As you can see, it reduced the expression NOT (NOT true) to true . Now that we have true = true we have to check it. For that we have to use one more tactic.

reflexivity

The reflexivity tactic is used to prove goals that assert equality between two terms or expressions. It asserts that any term is equal to itself, which is known as the reflexivity property of equality. When we execute reflexivity. , it checks if the LHS is equal to the RHS syntactically. If yes, we have proved the goal, otherwise we didn’t. Let’s see.

As you see from the above screenshot, now we have only one goal to prove. This is because we have proved our first goal ie. true = true. Now let’s prove our second goal, which is NOT (NOT false) = false.

Given the current knowledge, how would you prove it? Its exactly the same as how we solved our first goal. We’ll first simplify the expression and then check the equality. To simplify the expression we’ll use simpl. , once its simplified we’ll use reflexivity. to check the equality. Once we’ve executed these two tactics, this is what we get.

Congratulations, you’ve solved your first theorem. As you can see, there are no more goals to prove. Which means we’ve successfully solved/proved the property of NOT gate.

Proving AND gate property

Let’s first look at the theorem and break it down step by step.

Theorem and_property: forall (b c: bool),
    (AND b c) = (AND c b).
    Proof.
    intros b c.
    destruct b.
    - destruct c.
        + simpl. reflexivity.
        + simpl. reflexivity.
    - destruct c.
        + simpl. reflexivity.
        + simpl. reflexivity.
Qed.

What does the above theorem asks us to prove? It says that, for all b and c which is of type boolean, prove (AND b c) = (AND c b). What is AND? You can think of AND as a definition or function which takes in two arguments of type boolean and returns a boolean. Basically it does logical AND operation on the arguments and returns the result.

In simple terms, this is what we have to prove:

1. true = true
2. false = false
3. false = false
4. false = false

Now, let’s breakdown our proof step by step:

What’s the goal that we have to prove?

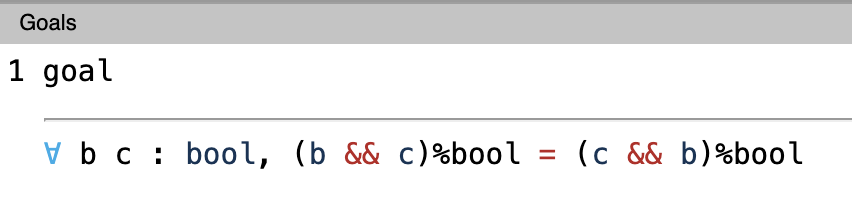
Currently we have one goal, as we prove, we’ll break it down into subgoals and prove it step by step. As always, the first step is to bring the variables into context. Here the variables are b and c. We know what tactic to use to introduce variables into the context.

intros

The line intros b c in our proof, brings the b and c variables into the context so that we can use them in subsequent tactics. This is what happens when that tactic gets executed.

destruct

We use destruct to breakdown our goals into small chunks. The line destruct b replaces b with true and false because that’s the type of b. And it breaks it into individual goals. This is how it looks once we execute destruct b.

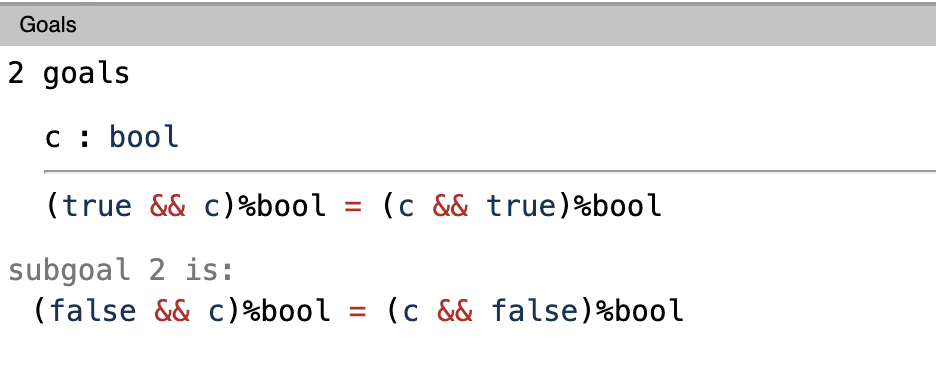
As you can see, it replaces b with true and false. The first goal is true case and the second goal is for false case.

The next line destruct c does the same thing for c, it replaces c with true and false. But since we’ve already broken down the goals before, executing this command won’t break it down further. You might have noticed the - sign before the destruct c command, we’ll get to it shortly. This is how it looks once we execute - destruct c.

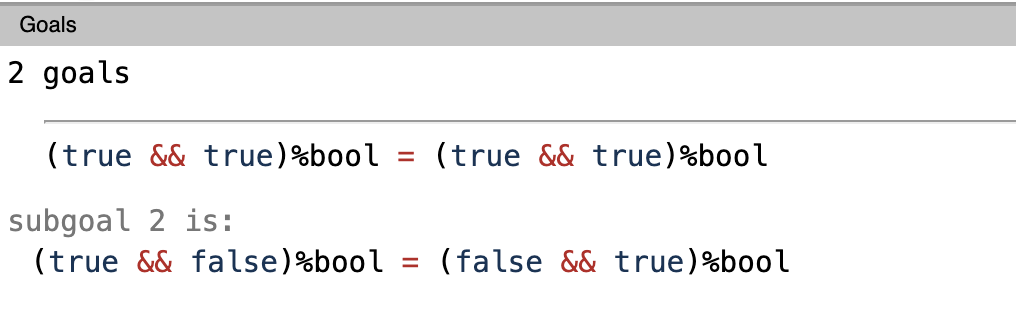
As you can see, both b and c got replaced with true and false. Now we can able to prove it one by one.

The line + simpl. reflexivity. , let’s break this down. What is + ? Just like - , plus(+) is used to focus on subgoals that we are gonna prove. Let’s what happens to the goal when we execute only +

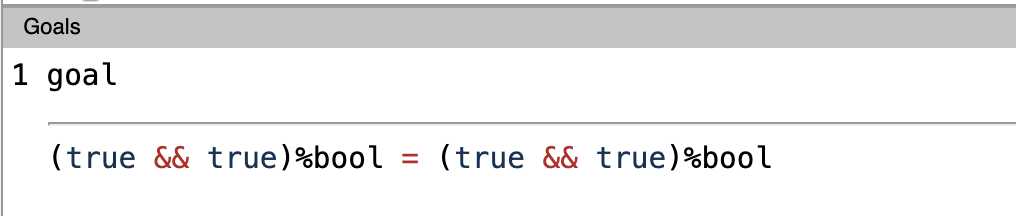
As you can see, previously we have two goals, now we have only one. Because + focuses on only one goal at a time. Now that we’ve got a goal to prove, let’s prove it.

From the original statement + simpl. reflexivity we’ve seen what + does. Now let’s look at simpl. Let’s try and execute simpl. and see what happens.

simpl

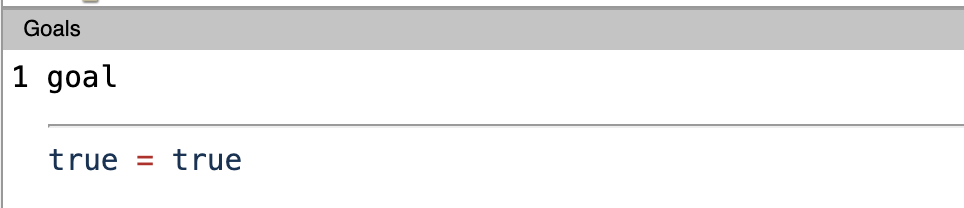
As the name suggests, it simplifies our statement/condition. Now we have true = true, which we know is equal. Can you guess what is the tactic we use to check equality?? You guessed it right.

reflexivity

Let’s execute reflexivity. and see what happens.

Reflexivity checks for equality. If LHS and RHS are equal, its success. Since we’ve proved our subgoal, Coq says we are done with our subgoal and we should be focusing on our next subgoal. To do that, we need to use the + symbol. Just like the previous subgoal we can use the same set of commands to solve the next subgoal. But let’s first see what’s our subgoal is.

Now that we know how to simplify the goal and check for equality let’s do that. Let’s execute simpl. reflexivity . Which first simplifies the statement and checks for equality.

It says, we’ve completed our subproof and asking us to focus on our goals. To do that, we should use -. But before that let’s recap what we’ve proved in our first two subgoals. So far, we’ve proved — true = true and false = false. We’ve couple more cases to prove, which are — false = false and false = false. That is what our next goal is gonna be.

Let’s focus on our next goal by executing -

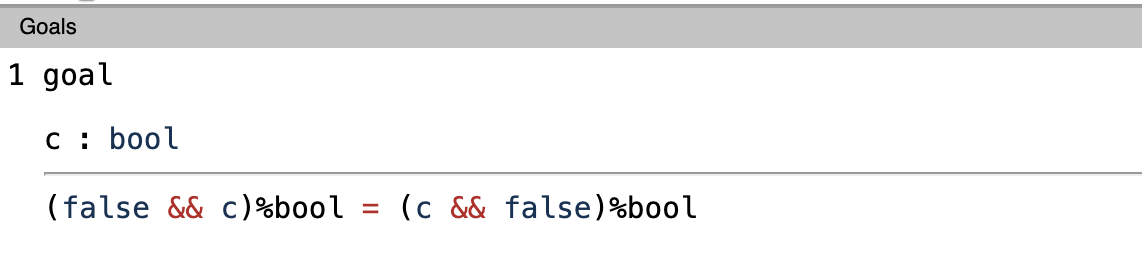
We’ve to expand c now, we can use the destruct tactic to do that. Executing destruct c. would give us:

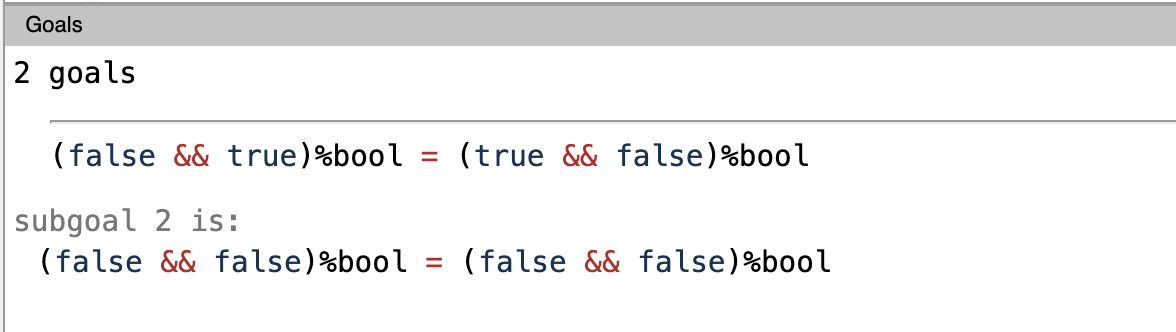
We’ve got two subgoals. We’ve seen a similar pattern before, when we were proving for b. The same way we prove these two subgoals. Executing the below statements would solve the proof.

+ simpl. reflexivity (* solves the 1st subgoal *)
+ simpl. reflexivity (* solves the 2nd subgoal *)

Voila! We have proved our theorem. As you can see, we’ve no more goals which means we have proved (AND b c) = (AND c b).

Armed with the basics of proving theorems, take on the challenge of proving (OR b c) = (OR c b). The steps mirror those we've used for solving (AND b c) = (AND c b). If you've grasped at least half of what I've shared, you've already achieved a great deal. Now, dive into theorem proving with confidence!